http://islamijati-web.blogspot.com/
Secara intuitif, teorema ini dengan sederhana menyatakan bahwa jumlah perubahan
infinitesimal suatu kuantitas terhadap waktu (atau terhadap kuantitas lainnya) akan menumpuk menjadi perubahan total kuantitas.
Untuk memahami pernyataan ini, diberikan sebuah contoh: Misalkan sebuah partikel berpindah mengikuti garis lurus dengan posisinya diberikan sebagai
x(
t), dengan
t adalah waktu dan
x(
t) berarti
x adalah fungsi dari
t. Turunan dari fungsi ini sama dengan perbuahan infinitesimal kuantitas, d
x, per perubahan infinitesimal waktu, d
t (tentu saja turunannya sendiri tergantung pada waktu). Didefinisikan pula perubahan jarak per perubahan waktu ini sebagai kecepatan
v partikel. Dalam
notasi Leibniz:
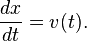
Dengan menata ulang persamaan ini, terlihat bahwa:

Dengan logika di atas, sebuah perubahan
x (atau Δ
x) adalah jumlah dari perbuahan infinitesimal d
x. Ia juga sama dengan jumlah dari hasil kali infinitesimal dari turunan dan waktu. Penjumlahahan takterhingga ini adalah pengintegralan; sehingga operasi penginteralan mengijinkan pemulihan fungsi semula dari turunannya. Dengan pemikiran yang sama, operasi ini juga dapat bekerja terbalik ketika kita menurunkan hasil dari sb\ebuah integral untuk memulihkan turunan semula.
[sunting] Pernyataan formal
Terdapat dua bagian teorema dasar kalkulus. Secara kasar, bagian pertama berkutat pada turunan sebuah
antiturunan, sedangkan bagian kedua berkutat pada relasi antara antiturunan dan
integral tertentu.
[sunting] Bagian pertama
Bagian ini kadang-kadang dirujuk sebagai teorema dasar kalkulus pertama.
Misalkan
f adalah fungsi bernilai real yang kontinu, didefinisikan pada sebuah
interval tertutup [
a,
b]. Misalkan juga
F adalah fungsi yang didefinisikan, untuk semua
x pada [
a,
b], dengan
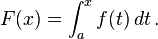
Maka
F adalah kontinu pada [
a,
b], terdiferensialkan (
differentiable) pada interval terbuka (
a,
b), dan

untuk semua
x pada (
a,
b)
[sunting] Bagian kedua
Bagian ini kadang-kadang dirujuk sebagai teorema dasar kalkulus kedua.
Misalkan
f adalah sebuah fungsi bernilai real yang kontinu, didefinisikan pada
interval tertutup [
a,
b]. Misalkan juga
F adalah
antiturunan dari
f, yakni salah satu dari fungsi-fungsi yang tak terhingga banyaknya yang untuk semua
x pada [
a,
b],

Maka
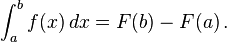
Misalkan
f adalah fungsi bernilai real yang didefinisikan pada sebuah
interval tertutup [
a,
b]. Misalkan juga
F adalah sebuah fungsi yang untuk semua
x pada [
a,
b],

Maka untuk semua
x pada [
a,
b],

dan

Misalkan kita perlu menghitung
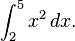
Di sini,
f(x) = x2 dan kita dapat menggunakan

sebagai antiturunan. Sehingga:
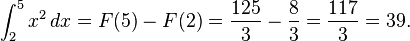
Atau lebih umumnya, misalkan kita perlu menghitung
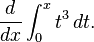
Di sini,
f(t) = t3 dan kita dapat menggunakan

sebagai antiturunan. Sehingga:
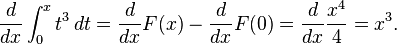
Namun hasil ini akan lebih mudah didapatkan apabila menggunakan:

[sunting] Pembuktian bagian pertama
Andaikan

Misalkan terdapat dua bilangan
x1 dan
x1 + Δ
x pada [
a,
b]. Sehingga didapatkan

dan
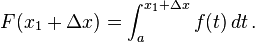
Pengurangan kedua persamaan di atas menghasilkan
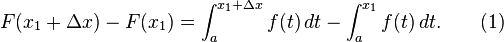
Bisa ditunjukan bahwa

- (Jumlah dari luas wilayah yang bersampingan sama dengan jumlah kedua wilayah yang digabungkan.)
Dengan memanipulasi persamaan ini, kita dapatkan
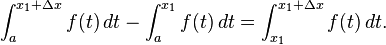
Substitusikan persamaan di atas ke (1), sehingga
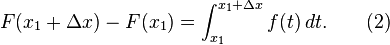
Menurut
teorema nilai antara untuk pengintegralan, terdapat sebuah
c pada [
x1,
x1 + Δ
x] sehingga
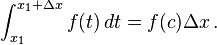
Substitusikan persamaan di atas ke (2), kita dapatkan

Bagi kedua sisi dengan Δ
x, menghasilkan
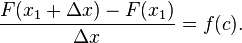
- Perhatikan pula ekspresi pada sisi kiri persamaannya adalah hasil bagi beda Newton untuk F pada x1.
Dengan mengambil limit Δ
x → 0 pada kedua sisi persamaan:
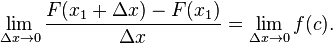
Ekspresi pada sisi kiri persamaan adalah definisi turunan dari
F pada
x1.

Untuk mencari limit lainnya, kita gunakan
teorema apit.
c ada pada interval [
x1,
x1 + Δ
x], sehingga
x1 ≤
c ≤
x1 + Δ
x.
Juga,
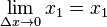
dan

Sehingga menurut teori apit,
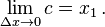
Substitusikan ke (3), kita dapatkan
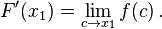
Fungsi
f kontinu pada
c, sehingga limit dapat diambil di dalam fungsi. Oleh karena itu, kita dapatkan
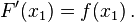
yang menyelesaikan pembuktian
(Leithold dkk., 1996)
[sunting] Pembuktian bagian kedua
Ini adalah pembuktian limit menggunakan
penjumlahan Riemann.
Misalnya
f kontinu pada interval [
a,
b], dan
F adalah antiturunan dari
f. Dimulai dengan kuantitas

Misalkan pula terdapat bilangan-bilangan
- x1, ..., xn
sehingga

Maka

Sekarang kita tambahkan setiap
F(
xi) bersamaan dengan balikan aditif (
inverse additive), sehingga kuantitas yang dihasilkan adalah sama:
![\begin{matrix} F(b) - F(a) & = & F(x_n)\,+\,[-F(x_{n-1})\,+\,F(x_{n-1})]\,+\,\ldots\,+\,[-F(x_1) + F(x_1)]\,-\,F(x_0) \, \\
& = & [F(x_n)\,-\,F(x_{n-1})]\,+\,[F(x_{n-1})\,+\,\ldots\,-\,F(x_1)]\,+\,[F(x_1)\,-\,F(x_0)] \,. \end{matrix}](http://upload.wikimedia.org/math/b/d/e/bde262027624d2d1b7d79d67751f9444.png)
Kuantitas di atas dapat ditulis sebagai penjumalhan berikut:
![F(b) - F(a) = \sum_{i=1}^n \,[F(x_i) - F(x_{i-1})]\,. \qquad (1)](http://upload.wikimedia.org/math/5/f/b/5fbb95b91da8e3ddceb869337d7323d5.png)
Kemudan kita akan menggunakan
teorema nilai purata. Dinyatakan dengan singkat,
Misalkan
F kontinu pada interval tertutup [
a,
b] dan terdiferensialkan pada interval terbuka (
a,
b). Maka terdapat
c pada (
a,
b) yang

Sehingga

Fungsi
F terdiferensialkan pada interval [
a,
b]; sehingga ia juga terdiferensialkan dan kontinu pada setiap interval
xi-1. Oleh karena itu, menurut teorema nilai purata,
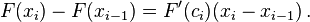
Substitusikan persamaan di atas ke (1), kita dapatkan
![F(b) - F(a) = \sum_{i=1}^n \,[F'(c_i)(x_i - x_{i-1})]\,.](http://upload.wikimedia.org/math/9/a/2/9a27d0ce017fd6a29ffc33d230617973.png)
Asumsi ini mengimplikasikan
F'(ci) = f(ci). Juga,
xi − xi − 1 dapat diekspresikan sebagai
Δx dari partisi
i.
![F(b) - F(a) = \sum_{i=1}^n \,[f(c_i)(\Delta x_i)]\,. \qquad (2)](http://upload.wikimedia.org/math/2/3/7/2371fea52b0fcdf7735b3d7eb5c7ef11.png)

Deret yang konvergen dari penjumlahan Riemann. Angka pada kanan atas adalah luas dari persegi panjang abu-abu. Ia konvergen ke intergal fungsi tersebut.
Perhatikan bahwa kita sedang menjelaskan luas persegi panjang, dengan lebar kali tinggi, dan kita menggabungkan total semua luas persegi panjang tersebut. Setiap persegi panjang, dengan
teorema nilai purata, merupakan pendekatan dari bagian kurva yang digambar. Juga perhatikan bahwa
Δxi tidak perlulah sama untuk setiap nilai
i, atau dengan kata lain lebar persegi panjang dapat berbeda-beda. Apa yang perlu kita lakukan adalah mendekatkan kurva tersebut dengan
n persegi panjang. Semakin kecil partisi ini dan semakin besar n, maka kita akan mendapatkan luas wilayah kurva yang semakin mendekati nilai sebenarnya.
Dengan mengambil limit ekspresi norma partisi mendekati nol, kita mendapatkan
integral Riemann. Yakni, kita mengambil limit partisi yang terbesar mendekati nol dalam hal ukuran, sehingga partisi-partisi lainnya lebih kecil dan jumlah partisi mendekati tak terhingga.
Maka kita mengambil limit pada kedua sisi (2). Kita dapatkan
![\lim_{\| \Delta \| \to 0} F(b) - F(a) = \lim_{\| \Delta \| \to 0} \sum_{i=1}^n \,[f(c_i)(\Delta x_i)]\,.](http://upload.wikimedia.org/math/2/9/1/291ffe044566ee45e9edf75a078f0a9e.png)
Baik
F(
b) maupuan
F(
a) tidak bergantung pada ||Δ||, sehingga limit pada bagian sisi kiri tetaplah
F(
b) -
F(
a).
![F(b) - F(a) = \lim_{\| \Delta \| \to 0} \sum_{i=1}^n \,[f(c_i)(\Delta x_i)]\,.](http://upload.wikimedia.org/math/c/5/7/c57e85d849c57c1ebd9f8c17a575c57b.png)
Ekspresi pada sisi kanan persamaan merupakan definisi dari integral terhadap
f dari
a ke
b. Sehingga kita dapatkan:
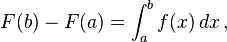
yang menyelesaikan pembuktian.
Kita tidak perlu mengasumsikan kekontinuan
f pada keseluruhan interval. Bagian I dari teorema menyatakan: Jika
f adalah setiap fungsi
terintegral Lebesgue pada [
a,
b] dan
x0 adalah bilangan pada [
a,
b] sehingga
f kontinu pada
x0, maka
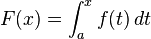
terdiferensialkan untuk
x =
x0 dengan
F'(
x0) =
f(
x0). Kita dapat melonggarkan kondisi
f lebih jauh dan andaikan bahwa ia hanyalah terintegralkan secara lokal/setempat. Pada kasus ini, kita dapat menyimpulkan bahwa fungsi
F terdiferensialkan
hampir di mana-mana dan
F'(
x) =
f(
x) hampir di mana-mana. Ini kadang-kadang dikenal sebagai
Teorema pendiferensialan Lebesgue.
Bagian II dari teorema adalah benar untuk setiap fungsi terintegral (
integrable fungction) Lebesgue
f yang mempunyai sebuah antiturunan
F (tidak semua fungsi terintegral mempunyainya).
Versi
teorema Taylor yang mengekspresikan suku galat (
error term) sebagai sebuah integral dapat dilihat sebagai sebuah perampatan (
generalization) dari teorema dasar.
Terdapat sebuah versi teorema untuk fungsi
kompleks: andaikan
U adalah himpunan terbuka pada
C dan
f:
U →
C adalah fungsi yang mempunyai sebuah antiturunan
holomorfik F pada
U. Maka untuk setiap kurva γ: [
a,
b] →
U,
integral kurva dapat dihitung sebagai
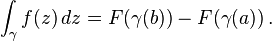
Teorema dasar dapat dirampatkan ke integral kurva dan permukaan pada dimensi yang lebih tinggi dan pada
manifold.
Salah satu pernyataan yang paling kuasa (
powerful) adalah
teorema Stokes: Diberikan
M sebagai
manifold mulus
sesepenggal dimensi n berorientasi dan
ω adalah sebuah bentuk
n−1, yakni
bentuk diferensial yang
disangga secara kompak pada
M kelas C
1. Jika ∂
M menandakan
sempadan M dengan
orientasi terinduksinya, maka
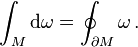
Di sini
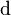
adalah
turunan luar yang hanya terdefinisikan menggunakan struktur manifold.
Teorema ini seringkali digunakan dalam situasi ketika
M adalah submanifold berorientasi terbenam (
embedded oriented submanifold) dari manifold yang lebih besar di mana bentuk
ω didefinisikan
[sunting] Catatan kaki
- ^ Lebih tepatnya, teorema ini berkutat pada integral tertentu dengan limit atas variabel dan limit bawah sembarang. Jenis integral tertentu ini mengijinkan kita menghitung satu dari banyak antiturunan sebuah fungsi (kecuali untuk yang tidak nol). Oleh karena itu, ia hampir setara (ekuivalen) dengan integral taktentu, didefinisikan oleh kebanyakan penulis sebagai sebuah operasi yang menghasilkan salah satu antiturunan sembarang sebuah fungsi, meliputi yang tidak nol.
- ^ See, e.g., Marlow Anderson, Victor J. Katz, Robin J. Wilson, Sherlock Holmes in Babylon and Other Tales of Mathematical History, Mathematical Association of America, 2004, p. 114.
- Larson, Ron, Bruce H. Edwards, David E. Heyd. Calculus of a single variable. 7th ed. Boston: Houghton Mifflin Company, 2002.
- Leithold, L. (1996). The calculus 7 of a single variable. 6th ed. New York: HarperCollins College Publishers.
- Malet, A, Studies on James Gregorie (1638-1675) (PhD Thesis, Princeton, 1989).
- Stewart, J. (2003). Fundamental Theorem of Calculus. In Integrals. In Calculus: early transcendentals. Belmont, California: Thomson/Brooks/Cole.
- Turnbull, H W (ed.), The James Gregory Tercentenary Memorial Volume (London, 1939)
[sunting] Pranala luar
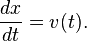

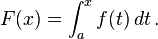


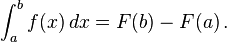


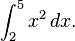
 sebagai antiturunan. Sehingga:
sebagai antiturunan. Sehingga: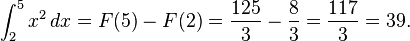
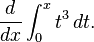
 sebagai antiturunan. Sehingga:
sebagai antiturunan. Sehingga: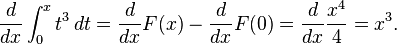



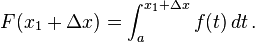
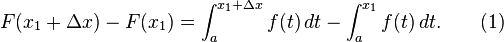

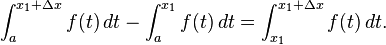
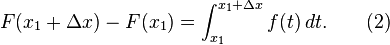
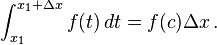

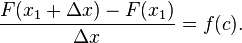
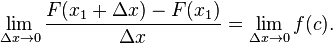

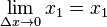 dan
dan 
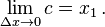
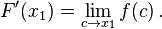
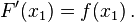



![\begin{matrix} F(b) - F(a) & = & F(x_n)\,+\,[-F(x_{n-1})\,+\,F(x_{n-1})]\,+\,\ldots\,+\,[-F(x_1) + F(x_1)]\,-\,F(x_0) \, \\
& = & [F(x_n)\,-\,F(x_{n-1})]\,+\,[F(x_{n-1})\,+\,\ldots\,-\,F(x_1)]\,+\,[F(x_1)\,-\,F(x_0)] \,. \end{matrix}](http://upload.wikimedia.org/math/b/d/e/bde262027624d2d1b7d79d67751f9444.png)
![F(b) - F(a) = \sum_{i=1}^n \,[F(x_i) - F(x_{i-1})]\,. \qquad (1)](http://upload.wikimedia.org/math/5/f/b/5fbb95b91da8e3ddceb869337d7323d5.png)


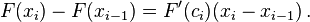
![F(b) - F(a) = \sum_{i=1}^n \,[F'(c_i)(x_i - x_{i-1})]\,.](http://upload.wikimedia.org/math/9/a/2/9a27d0ce017fd6a29ffc33d230617973.png)
![F(b) - F(a) = \sum_{i=1}^n \,[f(c_i)(\Delta x_i)]\,. \qquad (2)](http://upload.wikimedia.org/math/2/3/7/2371fea52b0fcdf7735b3d7eb5c7ef11.png)

![\lim_{\| \Delta \| \to 0} F(b) - F(a) = \lim_{\| \Delta \| \to 0} \sum_{i=1}^n \,[f(c_i)(\Delta x_i)]\,.](http://upload.wikimedia.org/math/2/9/1/291ffe044566ee45e9edf75a078f0a9e.png)
![F(b) - F(a) = \lim_{\| \Delta \| \to 0} \sum_{i=1}^n \,[f(c_i)(\Delta x_i)]\,.](http://upload.wikimedia.org/math/c/5/7/c57e85d849c57c1ebd9f8c17a575c57b.png)
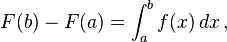
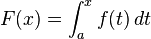
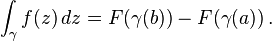
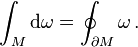
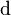 adalah
adalah